成果公报
华南师范大学心理学院张敏强教授主持完成了课题“高考‘一年多考’的‘分数等值’研究与实践”(GFA111009)。课题组主要成员为:王蕾、关丹丹、焦丽亚、黎光明、简小珠、方杰和张洁婷。
- 内容与方法
1 研究内容
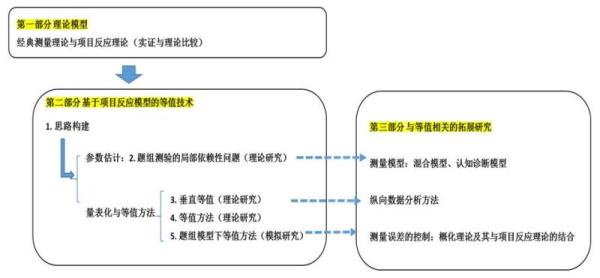
本项目通过研究及模拟数据实验找到一种有理论基础、为广大考生所接受的“分数等值”方法,并应用于“一年多考”的高考实践中去,以解决“一年多次考试”的不同难度的考卷分数比较及转换。基于此研究目的,开展以下研究。
(1)研究经典测验理论(CTT)和项目反应理论(IRT)在规模考试中“分数等值”的理论依据,分别基于两种测验理论探讨适用于大规模考试的“分数等值”理论,并进行实证比较。
(2)基于IRT模型在测验等值中的应用优势,进一步探讨IRT模型框架下的等值方法。
通过以下子研究达到目的:
1构建测验等值的流程化思路;
2探讨题组测验局部依赖性的模型解决方法,优化测验等值的参数估计步骤;
3比较和归纳量表化与等值方法,为等值方法的选用提供参考性建议。
(3)针对测量模型的优化、等值误差的测量与控制以及测验数据的纵向特点,分别对测量的方差分量估计、混合模型和认知诊断模型的应用与纵向数据分析方法进行拓展研究。
本课题研究思路如下:
2研究方法
本研究在各等值理论方法的比较归纳基础上,结合使用实证研究与模拟研究对各等值方法进行比较。
2.1 等值方法
2.1.1基于经典测量理论的等值方法
经典测验理论(Classical Test Theory, CTT)假设能力特质是潜在而相对稳定的,某能力特质的真正水平的数值为真分数T,实测的结果(即观察分数X)会围绕着真分数随测量的随机误差(E)而在某范围内波动,即观察分数是真分数和随机误差分数的线性组合。在CTT理论框架下构成了信度、效度、难度和区分度这四个指标对测验的质量和特性进行评价,分别反映测验的稳定性、有效性和测验项目的难易程度、区分能力。基于CTT的传统等值方法包括平均数等值(equi-mean equating)、线性等值(linear equating)、等百分位等值(equi-percentile equating)等。
2.1.2 基于项目反应理论的等值方法
项目反应理论(Item Response Theory, IRT),又称潜在特质理论,采用非线性模型(如Logistic模型或Samjima等级模型等),建立考生对题目的作答反应(即observed score)与潜在特质(即ability)之间的非线性关系。该测验理论有两大基本假设:1对考生所测试的潜在能力具有单维性;2在考虑了考生的能力之后,考生对各个项目的反应是相互独立的(即局部独立性)。项目反应最大的特点是,考生的能力估计不依赖于项目的难度参数,即考生的分数不会由于试题的难或容易而产生高估或低估。基于IRT的等值方法在数据收集后根据题目和数据类型选择合适的IRT模型(如单参数logistic模型、Samjema等级模型)进行IRT参数估计;然后使用某种方法,如动差方法(moment methods)、特征曲线转换方法(characteristic curve method)、同时校准方法(concurrent calibration)进行IRT量表转换,使参数估计置于同一个量尺上;最后进行测验原始分数向量表分数的转换。
2.2 Monte Carlo模拟研究方法
Monte Carlo模拟方法已经在应用物理、原子能、固体物理、化学、生物、生态学、社会经济学以及经济行为等领域中得到广泛应用。特别是在计算机上用Monte Carlo模拟方法解决很多理论和应用科学问题,在很大程度上可以替代许多大型的、难以实现的复杂实践或社会行为过程(杨自强, 2007)。
- 结论与对策
1 基于两种测量理论的等值方法比较
通过实证与理论研究,对经典测量理论与项目反应理论下的等值方法进行比较,得到如下结论。
经典测验理论的测验等值方法存在不少困难与局限:首先,它们确定的转换关系依赖于样本,会随被试样组的不同而变化,等值条件的唯一性(不变性)要求不能满足,无论哪种方法,都难以确保求出的转换关系是对称的、公平的。其次,经典测验等值方法应用重点又都在被试观察分数等值上,很难妥善解决难度、区分度这类项目参数等值的问题。最后,更重要的是,即使在线性等值的情况下,经典等值理论所认定的应予等值的测验分数间的线性转换关系,也是假设能够存在的,而不是必然能够具有的。项目反应理论却根本不同,在所选反应模型与实测资料适合良好的情况下,按项目反应理论方法所确定的被试特质与项目参数间的转换关系,就是必然应该具有的,这是因为特质与项目参数本应具有不变性。也正由于转换关系是来自模型的理论性质本身,所以,能够保证全面地较好满足唯一性、公平性、对称性等要求。另外,由于项目反应理论能同时估出特质与项目参数,特别是,项目难度又是直接定义在特质参数量纲上,因而,就能同时解决特质水平与项目参数的等值问题。所以,项目反应理论等值不仅在理论上具有优良的性质,而且在实用上具有极强的功能。项目参数等值问题的解决为大型题库的建设提供了有力的技术保证。
因此,本项目进一步重点对IRT理论框架下的等值方法进行研究。
2 基于IRT的等值技术
2.1 IRT测验等值的流程化操作思路构建
测验等值是测验研究中相对薄弱的一个环节,许多重要的考试都尚未实现统计等值。造成这种窘境的原因,皆因等值操作困难化。在参考国内外关于测验等值的相关文献的基础上,构建出IRT测验等值的流程化操作思路,包括等值设计、数据收集、参数估计、量表化及测验等值等五个步骤,如下图所示。
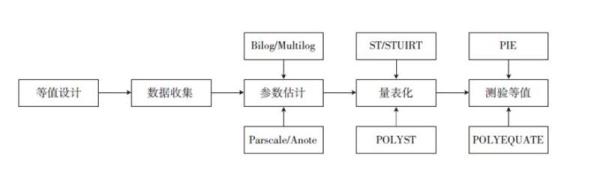
进一步,对参数估计、量表化和测量等值环节作方法上改进。
2.2 题组测验中处理局部项目依赖性(LID)的模型发展
在教育和心理测验领域中,题组是常用的测验建构、测验实施和评分的单元。题组(Testlet)是指共用同一个背景材料的一组题目(Rosenbaum, 1988)。由于同一题组内的多个题目共用一个刺激材料, IRT模型的局部项目独立假他设往往难以满足(Rosenbaum, 1988),出现局部项目依赖。局部项目依赖(Local Item dependence, LID)是指对于特定能力的被试,其在某个题目上的作答影响在其他题目的作答或受其他题目作答情况的影响。
本研究在评述题组测验中处理LID的标准IRT方法、多级评分IRT方法、题组随机效应方法和两因子方法的基础上,以参数估计精度作为准则,对这4 种处理LID方法的效果和适用条件进行了归纳并作出相应的评析。
依据前人关于处理LID方法的研究,总结如下:(1)当题组长度较短(4-6个题目)且题组型题目所占比例较小时,可以采用标准IRT模型进行数据分析;(2)当题组LID为中等程度且测验包含很大部分相互独立项目时,采用多级计分IRT模型来处理LID也是可以的;(3)当题组存在较大LID时,应当采用TRT模型和两因子模型。二者各有优点,相比两因子模型, TRT模型更节俭,但两因子模型参数估计软件运行更加简单和高效。但是,如果测验中存在局部独立项目,采用TRT模型会得到更为精确的参数估计值。
2.3 IRT与MIRT在测验垂直等值中的应用
常用的测验等值是水平等值(horizontal equating),是对测量同一心理特质的多个测验形式进行分数转换,要求各个测验形式之间具有同质性、等信度、难度相近、对称性、样本不变性等特点。但是,在实际应用中,常面临多个测验的难度水平有明显差异,或被评价团体的能力水平差异较大等情况。垂直等值(vertical equating)则是针对这种情况的等值,将测试同学科、同一种心理特质的不同水平测验转换到同一个分数量尺上。它要求测验具有相似结构与高信度,但不要求测验难度相同、被试水平一致。IRT与MIRT是实现垂直等值的主要方法。
IRT的垂直等值步骤及其适用方法总结如下。
(1)模型选择。研究者通常根据数据类型、参数估计精度和等值误差选择合适的IRT模型进行垂直等值。主要有:用于0-1 计分测验的单参数、两参数以及三参数逻辑斯蒂克模型,用于多级计分的测验的等级反应模型(Graded Response Model)、分部评分模型(Partial Credit Model)、拓广分布评分模型(Generalized Partial Credit Model)、称名反应模型(Nominal Response Model)和评定量表模型(Rating Scale Model)。
(2)参数估计与标定。通过标定把不同的能力测验转换到同一尺度上, 即构建共同量表。常用的标定方法有同时标定(concurrent calibration)和分别标定(separate calibration)。
(3)最常用的能力分数估计方法有极大似然估计(maximum likelihood estimates, MLE)、期望后验估计(expected a posteriori, EAP)和极大后验估计(maximum a posteriori, MAP)。
MIRT是在IRT和因素分析的基础上发展起来的一种测验理论。两者方法和步骤类似,但仍存在以下区别:首先,模型选择方面,IRT适合单维数据,MIRT适合多维数据;其次,标定方法选取方面,数据满足单维性假设时,同时标定更具优势,一旦数据无法满足单维性假设,若采用IRT方法,分别标定优于同时标定,若采用MIRT方法,同时标定则更具优势;第三, 能力估计方法方面,关于IRT方法的研究较多,MIRT相关的研究较少。
2.4 非等组锚题设计的IRT等值方法及其应用分析
本研究在非等组锚测验设计下,根据前人的模拟与实证研究,针对常用的0-1计分三参数IRT模型,对的同时参数标定(CC)、线性参数转换(LSC)和固定参数标定(FIPC)这三大类等值方法的优缺点总结归纳如下。
(1)当锚题数量为中等或较大水平时,群体能力分布没有差异或差异很小时,CC和LSC的等值效果都很好,测验工作者可根据实际需要等值到哪个量尺上来选择不同的方法:当需要等值到基准组被试群体的量尺上时,可选用LSC;当需要等值到基准组和目标组合并后的被试群体的量尺上,应选用CC。
(2)当锚题数量为中等或较大水平时,若群体能力分布差异较大时,采用CC等值效果更佳,若需转换到基准测验量尺上,可先采用CC方法估计出项目参数,再采用矩估计法转换到基准测验量尺上。
(3)当锚题数量为较小水平时,使用LSC中的特征曲线法时等值效果较好。
(4)当构建大型题库时,采用FIPC更为灵活、有效、省时。
(5)样本量越大,不同等值方法的差异越小,当样本量较大时(一般为3000左右),不同等值方法的等值精度均较高,且差异很小,测验工作者可灵活选择等值方法,若对等值样本量没有信心,可参照上述四条选择合适的等值方法。
2.53PLM和3PTM对题组测验的参数等值比较研究
考虑题组形式在实际考试中的普遍性和意义,本课题基于前人研究以及课题前阶段的研究成果,引进基于题组的TRT模型-三参数题组模型(3 Parameters Testlets Model, 3PTM)。该模型由三参数逻辑斯蒂模型(3 Parameters Logistic Mode, 3PLM)加入了与每个题组相关的随机影响参数扩展而来的,考虑了题组测验中的局部依赖性。对其与3PLM的参数等值效果进行比较,考察3PTM在题组等值中是否具有优越性。
本研究给出了利用IRT特征曲线法求解等值系数的方法和具体步骤。以等值系数估计值的误差大小作为衡量标准,以Wilcoxon符号秩检验为依据,进行了Monte Carlo模拟实验。实验结果表明,对含题组的测验等值:
(1)从被试人数、题组相依性程度,猜测度等方面比较3PTM和3PLM用于题组等值的效果,表明考虑了局部相依性的题组模型3PTM绝大部分情况下都比未考虑相依性的局部独立模型3PLM等值更为精确,绝大部分情况下优势显著。
(2)采用6种不同的等值准则对3PTM对题组测验的等值进行研究。研究结果表明,等值系数A取值0.5-1.0之间时,SLcrit表现优于其他的等值准则。A取值为1.4-2.0之间时,Hcrit的表现最好,SQRcrit在A取值1.0-1.3之间时表现较好。SREcrit、COScrit、Wcrit占优的情况不多,胜出的范围也没有规律。
3 与等值相关的一些基础研究
针对等值误差的控制、垂直等值和等值的测验模型等问题,本项目拓展了与等值相关的基础研究。
3.1概化理论的方差分量估计
本部分研究主要探讨改善GT方差分量估计,为各种分数分布形态下测量误差的估计及误差来源的控制提供更精确的方法,进而优化等值误差。结论如下:
(1)在各种参数分布形态下,采用GIRM模型进行IRT参数估计和GT方差分量估计是可行的;在被试能力参数为标准正态分布时,GIRM模型对被试变异的估计准确性高于传统GT方法,但在均匀分布和伽马分布下略差于传统GT方法;在题目难度参数为偏态分布时,GIRM方法对题目变异估计的准确性不及传统GT方法。
(2)Traditional方法估计正态分布和多项分布数据的方差分量相对较好,估计二项分布数据需要校正,Jackknife方法准确地估计了三种分布数据的方差分量,校正的Bootstrap方法和有先验信息的MCMC方法估计三种分布数据的方差分量结果较好。
(3)关于方差分量估计及方差分量估计变异量的研究结果,不论何种数据分布形态,Bootstrap方法最优,校正的Bootstrap方法相比未校正的Bootstrap方法估计结果更为可靠。
3.2纵向数据方法探讨
“一年多考”所涉及的垂直等值需要考虑数据的纵向性分析以及数据的整合分析。因此通过对纵向数据的方法性研究,开拓垂直等值的统计分析思路。结论如下:
(1)对于追踪研究的方法,样本量、测量次数和持续时间应依据理论模型和研究条件确定,当样本量受限,可适当增加测量次数和持续时间降低对样本量的要求,但样本量和测量次数应满足理论模型和统计模型的最低要求。对数据缺失问题可从研究设计、研究过程和缺失原因分析等多方面进行准备和干预。
(2)加速追踪设计(ALD)可以在大型发展心理、教育研究的应用,这不但具有ALD的其他优点, 而且可获得更广泛的信息, 有利于系统探索复杂心理与行为发展的外在和内在影响因素及作用机制。
(3)整合数据分析(IDA)有以下优点:1提高了结论的论证强度和效应的评估力度;2增加样本的异质性,提高研究的外在效度;3构建广泛的心理评估,提高对心理结构的评估力;4扩展发展研究的时间段。
3.3混合模型在测验中的应用
混合模型与测量模型的结合有助于考虑测验中的个体质化差异,使模型更贴近实际的测量数据。因此,对混合模型的理论、方法、应用以及与测量模型的结合展开研究。结论如下:
(1)基于混合因素模型的方法是潜变量空间研究的主导趋势之一,而模型选择是判断潜变量空间的关键。模型选择主要受类别间的重叠程度、外显变量数目、计分方式和样本量的影响,对群组分类时应根据群组下的平均样本量nk选择模型指标。当nk≥40时,首选AIC3,其次是BIC,且nk最好达到50;当nk≤30时,建议选用BIC*或AIC,但无法保证很高的正确率。此外,在抽样中,尽可能详细地记录各种人口学变量,进而考虑群组水平样本的差异。
(2)混合IRT 在IRT 与LCA 的基础上继承和发展了新的优势:不仅可以通过构造分类潜变量发掘潜在的类别,还可以对不同潜在类别之间的连续潜变量进行对比研究。同时,与传统的DIF 分析方法相比,可以提炼出被试的潜在分类信息, 而不用事先假定被试的分组信息。
- 成果与影响
本项目针对高考“一年多考”的分数等值问题展开一系列的理论和方法研究。首先对基于两大测量理论下的等值方法进行比较,发现IRT等值方法的优点。然后,进一步对IRT的等值思路流程进行梳理,总结出等值的五大步骤,分别是等值设计、数据收集、参数估计、量表化及测验等值。这五步骤中的每一步所采取的方法都会影响等值的结果,其中,对于高考这种大规模考试形式基本上确定了等值设计与数据收集的方法,而对于参数估计、量表化和测验等值的方法还有待研究,这也是本项目的研究问题的关键。一方面,通过改善测量模型,来提高参数估计的精确度,例如建立适用于题组测验的题组项目反应模型,适用于垂直等值的多维项目反应模型,适用于能力的混合分布,根据不同的计分方式选择罗吉斯蒂模型、等级反应模型等。另一方面,对于等值方法的选取,需要根据锚题数量、群体能力分布差异等因素“分而治之”。此外,还基于概化理论这一现代测量理论,对测量误差的估计以及误差来源的控制提供更精确的方法,为等值误差的估计与控制提供研究的理论和技术铺垫。
本项目一般结论为:
第一,对于高考“一年多考”的分数等值,可以基于经典测量理论,通过原始分转换为标准分并使用线性转换的方法进行等值,只要对考试难度做较好的控制,等值的结果可靠,并易于被考生接受。
第二,采用IRT的理论方法,有效地控制测量误差,建立题库,入库题目可以采用本研究中提供的等值方法,建设基于项目反应理论的项目参数等值的考试题库,在编制试题时选用等值的题目组成试卷,从而实现报告分数的等值。
- 改进与完善
本项目重点对等值中的参数估计与等值方法进行理论与应用研究,对于方法的理论探索,还可在以下方面进行改进完善:
第一,对不同的等值方法的比较,未来可考虑高考的不同题型(0-1记分,多级记分,混合题型,题组题型)和数据分布所形成的不同IRT模型,并基于不同模型下对等值方法进行更系统的比较。
第二,对于不同等值方法得到的等值函数,还可以通过求取等值函数均值的方法得到新的等值函数,以减少等值误差,提高等值稳定性。未来的模拟研究可将求取等值函数均值的方法,与CC、LSC和FIPC进行比较研究。
第三,对于含题组的测验等值问题,目前仅考察了被试人数、题组相依性以及猜测度等影响因素,还有其他一些影响因素如题组数量、参数估计误差等,还可进一步探讨。对于更为复杂的多级评分模型,如何与题组模型相结合,也是值得将来深入研究的问题。
第四,对于垂直等值,未来研究应纳入更多变量条件进行比较研究, 拓展方法的应用。同时,垂直等值现阶段多是在直接等值(direct equating)的条件下进行的,对于间接等值(indirect equating)下不同等值方法还有待系统比较。
此外,虽然多数模拟研究会采用等值结果对真值的修复程度、RMSD等指标,但是等值效果的评价标准问题一直是等值研究中的难点,不同的研究采用的评价标准不完全一致,确定或者寻找一种评价等值研究的一致评价标准是值得进一步研究的议题。
五、成果统计一览表(请按下页的“课题组成果统计一览表”栏目填写完整)
课题组成果统计一览表
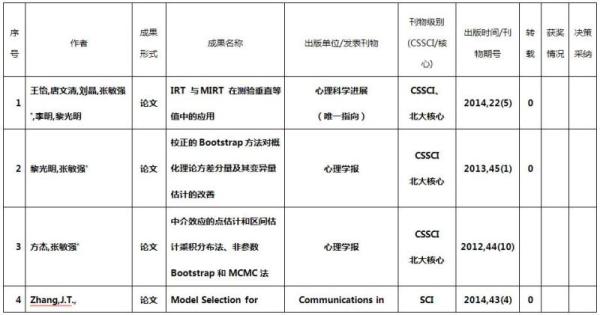
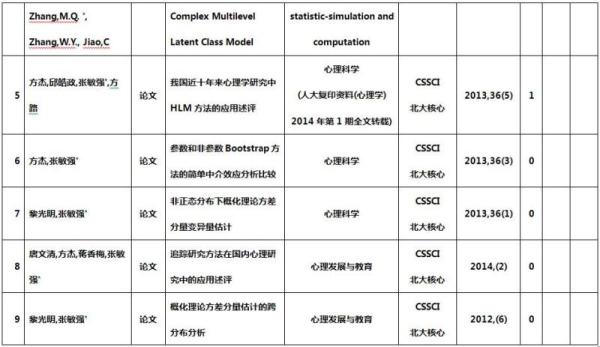
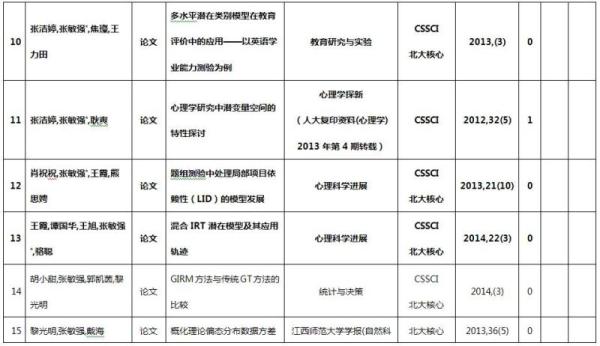
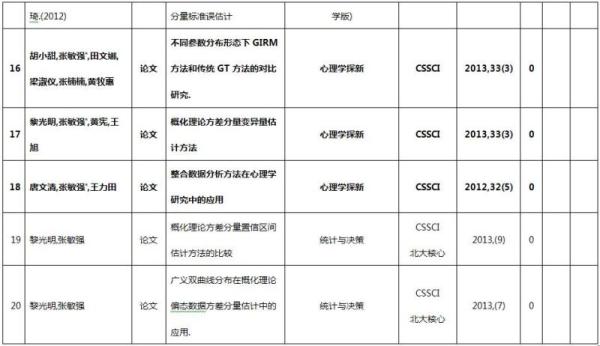
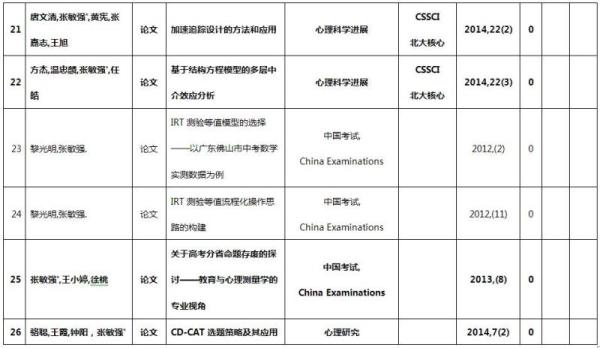
本项目完成了由此项目资助的学术论文共28篇,其中《IRT与MIRT在测验垂直等值中的应用》是唯一指向的成果。在发表的论文中,CSSCI论文21篇(2篇《心理学报》),SCI 1篇;此外,硕士论文1篇。参加国际会议1次,共被收录论文23篇,同时被SSCI杂志摘要收录;参加国内学术会议2次,共被收录论文26篇。在学术期刊发表的论文列表如下,其中由负责人作为第一作者或通讯作者的文章有21篇(粗体标注):
注:* 为通讯作者。
1.“成果形式”请注明为论文、编著、专著或教材
2.“获奖情况”请填写政府颁发的、省部级二等奖以上的奖励,奖项名称应与课题名称对应。
3.“决策采纳”指被省部级以上党政领导机关完整采纳吸收,并附有基本材料和相关证明。


 首页
首页 京公网安备 11040202430017号
京公网安备 11040202430017号